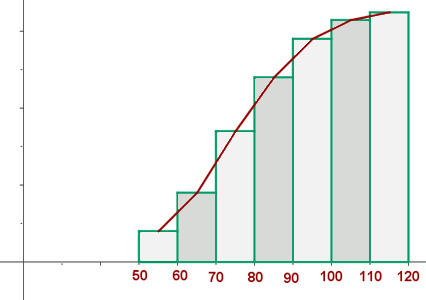
Ciencia que proporciona técnicas para tratar gran volumen de datos para extraer y mostrar la información que subyace en ellos. Permite obtener información de un colectivo muy amplio de datos a partir de un conjunto relativamente pequeño de datos procedentes de él, gracias a ello se formulan modelos matemáticos que representen la repuesta obtenida en alguna característica de interés al ser influenciada por diferentes factores. Con esta información en la mano se puede tomar decisiones cuando exista un marco de incertidumbre.
En Estadística se estudian fenómenos aleatorios, que son aquellos cuyo resultado no es previsible aunque se repitan en idénticas condiciones.Moda: es la categoría, valor o marca de clase que más se repite. Cuando tengamos datos de tipo contínuo solo tendrá sentido la moda después de haber sido agrupados en clases.
La moda de la variable Replantado es N, pues su frecuencia es la mayor entre las dos categorías posibles. La moda de la variable Grado de afección es M, en tanto que para la variable Nº de ramas primarias hay dos valores con máxima frecuencia, son 1 y 2 ramas.
La moda puede no ser única, y hablamos de distribuciones de frecuencias bimodales, trimodales, etc.
Mediana: es aplicable a datos como mínimo ordinales, y se define como aquél valor de la variable que ocupa la posición central del conjunto de datos ordenados, también se puede definir como aquél valor de la variable que resulta ser mayor o igual que la mitad de los datos y menor que la otra mitad.
Cuando se considera los N datos sin agrupar, la mediana es el dato que ocupa la posición (N+1)/2, de los datos ordenados.
Si el número de datos N es impar la mediana se calcula de modo inmediato, si el número de datos es par, la mediana es la media aritmética de los datos que ocupan las posiciones N/2 y N/2 + 1.
Media: solo es aplicable a datos de tipo numérico, es la media aritmética de los datos observados, o sea, la suma de todos ellos dividido por el número de observaciones:
para datos sin tabular, si están tabulados en tablas de frecuencias:
, siendo k el número de valores distintos y ni la frecuencia absoluta correspondiente al valor xi de la variable.
